Aula 01 - Noções básicas

Slides dessa aula

Script dessa aula

R como calculadora

A linguagem do R é um tanto quanto intuitiva, muita coisa sai do jeito certo no chute! Para ver um exemplo disso, é interessante começar fazendo do R uma grande calculadora. Tente jogar no console 2*2 - (4 + 4)/2. Pronto. Com essa simples expressão você já é capaz de imaginar (e certeiramente) como pedir ao R para fazer qualquer tipo de operação aritmética. Lição aprendida!

Além do mais, as operações e suas precedências são mantidas como na matemática, ou seja, divisão e multiplicação são calculadas antes da adição e subtração. E os parênteses nunca são demais!

Falando em matemática, o \(\pi\) já vem definido!

pi

## [1] 3.141593

sin(pi/2) + 2*3

## [1] 7

(sin(pi/2) + 2)*3

## [1] 9

Veja que apareceu a função sin(), o famoso seno. Tente outras funções trigonométricas para ver se acerta de prima!

Mas a ideia é essa. Ser intuitivo. A dica aqui é tentar! No R, um erro não é nenhuma dor de cabeça, é rápido consertar e testar (debugar, para os mais íntimos).

Valores especiais

Certas operações matemáticas podem suscitar em valores não numéricos. Exemplo disso são log de números negativos e divisões por zero. Para tais operações, o R reservou valores especiais para serem retornadas quando operações não resultarem em um número propriamente dito. A tabela abaixo lista esses objetos:

Operadores aritméticos

Os bons e conhecidos operadores aritméticos. Com números reais eles funcionam como na matemática, mas ao saírmos da reta, eles podem fazer muito mais!

Exemplos:

1 + 1

## [1] 2

10 - 8

## [1] 2

2*10

## [1] 20

18/3

## [1] 6

2^4

## [1] 16

9%%2

## [1] 1

9%/%2

## [1] 4

Operadores lógicos

Operadores lógicos retornarão sempre ou TRUE ou FALSE. Eles definem perguntas que aceitam apenas verdadeiro e falso como resposta, como sugere o quadro abaixo.

Exemplos:

Números complexos

O R manipula números complexo de maneira fácil e intuitiva do mesmo jeito que trata os números reais. Além disso, disponibiliza funções úteis para eles, como módulo, conjugado e argumento.

z <- -8 + 0i

# verifica se z é um número commplexo
class(z)

## [1] "complex"

is.complex(z)

## [1] TRUE

A tabela abaixo resume algumas funções interessantes para números complexos.

Demais funções matemáticas, como logaritmo, funções trigonométricas, exponencial e radiciação também estão implementadas para números complexos.

Controle de fluxo (flow controls)

Sumário

• if, else, else if: testa uma condição
• for, while: "laços" ou iterações
• break, next: ações dentro de laços

if, else e else if

Estrutura:

if(<condição1>) {
  # se a condição1 for verdadeira...
  # faz coisas interessantes.
} else if (<condição2>) {
  # caso a condição1 seja falsa e a condição2 seja verdadeira...
  # faz coisas legais para este caso.
} else {
  # faz coisas necessárias caso todas as condições anteriores falharem
}

As condições devem ser expressões lógicas, ou seja, testes que retornem TRUE ou FALSE. Assim, o código entre {} será executado se a condição for TRUE ou será ignorada se a condição retornar FALSE.

Exemplo:

x <- 4

# teste: x NÃO é um número?
!is.numeric(x)

## [1] FALSE

# teste: x é menor que zero?
x < 0

## [1] FALSE

# teste: x é maior que zero?
x > 0

## [1] TRUE

if(!is.numeric(x)) {
  "x não é um número"
} else if(x > 0) {
  "x é positivo"
} else if(x < 0) {
  "x é negativo"
} else {
  "x é nulo"
}

## [1] "x é positivo"

O que acontece no exemplo acima, passo a passo:

1. A expressão !is.numeric(x) testa se x NÃO é um número. Como x vale 4, ele retorna FALSE. Assim, a expressão {"x não é um número"} não é executada e a próxima condição é testada;

2. No primeiro else if, o teste lógico x > 0 retorna TRUE, fazendo com que a expressão {"x é positivo"} seja executada e todo o restante dos testes, ignorado.

OBS: a condições x < 0 nunca chegou a ser testada. Uma vez encontrada uma condição verdadeira, o programa executa o respectivo bloco de códigos entre {} e descarta as demais instruções.

Considerações:

• O else e o else if têm que estar na mesma linha do } da expressão anterior, senão não rodará!

# Certo
if(1 == 2) {
  "Um resultado muito interessante!"
} else { # <----- Mesma linha que o "}"
  "1 é diferente de 2"
}

# ERRADO!!! Não rodará
if(1 == 2) {
  "Um resultado muito interessante!"
}
else { # <----- Na linha abaixo do "}"
  "1 é diferente de 2"
}

• Além de TRUE e FALSE, o R aceita 1 e 0, respectivamente. Na verdade, não precisa ser 1 exatamente, a regra é:

  • número diferente de zero é TRUE; e
  • número igual a zero é FALSE.

• Objetos character, NA, NaN e list não são interpretáveis como lógicos. Será retornado um erro caso tente passá-los como condições.

• Caso seja passado um array, vector ou matrix, será utilizado apenas o primeiro elemento (é melhor evitar usar arrays como condições!). Será enviado um aviso de que isso ocorreu.

• else e else if são opcionais.

for

O for é um tipo "laço" (loop, em inglês) que aplica um bloco de código para um número fixo de iterações. Geralmente, um for percorre um vetor e utiliza um elemento diferente deste vetor em cada iteração.

Estrutura:

for(iterador in <sequencia>) {
  # Fazer algo para cada item da <sequencia>
  # pode ter outros for's aqui dentro!
}

Exemplo:

O uso mais simples é quando iteramos em um vetor de inteiros, como se fossem contadores.

for(i in 1:5) {
  print(i)
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5

Mas podemos iterar em um vetor qualquer.

frutas <- c("banana", "uva", "abacaxi")

# Brincadeira da <fruta> + "guei"
for(fruta in frutas) {
  print(paste(fruta, "guei", sep = ""))
}

## [1] "bananaguei"
## [1] "uvaguei"
## [1] "abacaxiguei"

Para cada item do vetor frutas, o for atribuiu ao objeto fruta o valor do respectivo item e aplicou a função print(paste(fruta, "guei", sep = "")).

Formas alternativas com o mesmo comportamento que o acima:

# repare nos []'s depois do vetor 'frutas'
for(i in 1:length(frutas)) {
  print(paste(frutas[i], "guei", sep = ""))
}

# seq_along() é uma função especialmente útil para for's
for(i in seq_along(frutas)) {
  print(paste(frutas[i], "guei", sep = ""))
}

OBS Apesar de parecer mais 'elegante' atribuir diretamente os valores ao iterador (como no caso do fruta in frutas), muitas vezes você se pegará na necessidade de usar os índices dos valores. Casos típicos é quando se tem um outro vetor que faz relação com outro. O exemplo abaixo não seria possível caso utilizássemos fruta in frutas no lugar de i in seq_along(frutas).

# Exemplo simples de quando é util utilizar índice em vez de valor.
frutas1 <- c("banana", "uva", "abacaxi")
frutas2 <- c("kiwi", "uva", "laranja")
pessoas <- c("Amanda", "Bruno", "Caio")

for(i in seq_along(frutas1)) {
  if(frutas1[i] == frutas2[i]) {
    frutas1[i] <- "manga" # Troca a fruta 1
    print(paste(pessoas[i], "ganhou frutas repetidas. Uma delas foi trocada por manga."))
  }
}

## [1] "Bruno ganhou frutas repetidas. Uma delas foi trocada por manga."

ifelse(): for com if else

Como veremos mais para frente, vetores são quase sempre bem-vindos no R. Muitas funções trabalham com vetores de maneira muito conveniente e a função ifelse() é um exemplo disso. Ela é a abordagem mais simples quando queremos que cada elemento de um vetor passe por algum teste lógico (como no exemplo acima) para retornar um valor dependendo se a condiçao for TRUE ou FALSE (como nunca é demais, dê um ?ifelse para ver a documentação se for preciso). Abaixo está a replicação do exemplo acima, mas sem a mensagem de aviso.

frutas1 <- c("banana", "uva", "abacaxi")
frutas2 <- c("kiwi", "uva", "laranja")
pessoas <- c("Amanda", "Bruno", "Caio")

frutas1 <- ifelse(frutas1 == frutas2, "manga", frutas1)

O código acima está dizendo que se os respectivos elementos de frutas1 e frutas2 calharem de serem iguais, então substitua por "manga". Se forem diferentes, então mantenha a fruta 1 original. Finalmente, atualize o vetor frutas1.

Na parte de vetorização será descrita com mais detalhe o que está acontecendo por trás dos panos.

Considerações:

O uso do for, ao contrário das outras linguagens de programação, se tornará cada vez menos frequente conforme você for se aprimorando no R. Ele é especialmente ineficiente no R e, além disso, existem outras funções que o substituem e ainda facilitam muito mais a vida.

while

O laço while é especialmente útil quando não sabemos quando iremos parar (a condição para o laço deixar de rodar pode envolver o acaso ou convergência, por exemplo). Cuidado com os loops infinitos! =)

Estrutura:

A estrutura é muito similar ao if. Tem a condição (ou teste lógico) e a expressão a ser executada enquanto a condição for verdadeira.

while(<condições>) {
  # coisas para fazzer enquanto as <condições> forem TRUE
}

Exemplo:

Abaixo está uma simulação de lançamento de moedas do qual se tem interesse em saber quantos lançamentos foram necessários até o aparecimento de uma "cara".

p <- 0.2 # probabilidade de cair "cara"
lances <- 0 # contador de lançamentos
while(runif(1) > p) {
  lances <- lances + 1
}

lances

## [1] 1

A função runif(1) gera um número aleatório no intervalo unitário toda vez que a condição é avaliada. Se este número for maior que p, então a moeda e lançada novamente e o contador de lançamentos é incrementado em uma unidade e esse ciclo se repete até que, por acaso, o número sorteado seja menor que p. No fim, teremos nossa desejada variável aleatória simulada de lances até "cara".

Repare que enquanto a condição retornava TRUE, a expressão sera reexecutada. O laço só parou quando a condição retornou FALSE. Essa é a regra do while.

Vetorização

Vetores no R são cadeias ordenadas de elementos (geralmente números ou palavras) e são os objetos de maior interesse porque são eles que guardam os dados a serem analisados. Por essa razão que quase tudo feito no R aceita de braços abertos um "vetor" (entre aspas por que "vetor" aqui pode ser vetor, matriz, tabela e afins, tipos de objetos que serão explicados em detalhes na próxima aula).

Se você é novo no mundo da programação, não vai sentir muito a vantagem desse conceito. Aos que já estão acostumados a programar em outras lingaguens de programação, se verão tentados a usar loops para tudo. Isso terá de mudar (e irá, naturalmente). Como frisado anteriormente, loops no R são sofrivelmente ineficientes.

Tecnicalidades

Tecnicamente, vetorização nada mais é do que a cultura de se criar e usar funções vetorizadas. Essas funções recebem vetor(es) [x1, ..., xn] e devolvem vetor(es) [f(x1), ..., f(xn)]. Mas por quê é importante, afinal?

Implementar funções vetorizadas seria uma tarefa simples, não fosse a lentidão dos loops. No R, funções vetorizadas realmente úteis são implementadas nas linguagens de baixo nível, que são muito mais rápidas. Por isso, a não ser que domine C, FORTRAN ou C++, você ficará dependente das funções vetorizadas disponíveis pelo R ou por terceiros.

Eficiência

Abaixo está um exemplo que mostra a diferença de tempo que leva para calcular a raiz quadrada de cada elemento de um vetor de números.

• Uma das funções está implementada inteiramente em R utilizando um for para calcular a raiz quadrada em cada elemento do vetor por meio da função sqrt();
• Uma segunda maneira de efetuar a mesma operação tira proveito da implementação vetorizada em C da função sqrt().

x <- 1:1000000 # sequência de inteiros de 1 a 1000000

# função que calcula a raiz quadrada de cada elemento de um vetor de números
meu_sqrt <- function(numeros) {
  resp <- numeric(length(numeros))
  for(i in seq_along(numeros)) {
    resp[i] <- sqrt(numeros[i])
  }
  return(resp)
}

# Comparação de eficiência entre função vetorizada e função "vetorizada no R"
system.time(x2a <- meu_sqrt(x))

##    user  system elapsed 
##   1.533   0.011   1.544

system.time(x2b <- sqrt(x))

##    user  system elapsed 
##   0.009   0.000   0.010

# Verifica que os dois vetores são iguais
identical(x2a, x2b)

## [1] TRUE

Um ganho de 100-200 vezes na eficiência! E as vantagens não param por aí:

1. Essas funções foram construídas e testadas por pessoas que ganham a vida fazendo isso;
2. No R, uma função é "esperta" e funciona para diferentes tipos de objetos que passamos a ela, muitas vezes da forma que esperamos.

Reciclagem

Um conceito que caminha junto com a vetorização é a chamada Reciclagem. Um exemplo ajuda a esclarecer o que isso significa.

x <- c(1,5)
y <- c(1,10,100,1000)
x + y

## [1]    2   15  101 1005

Neste exemplo estamos somando dois vetores de tamanhos diferentes. Na matemática isso não faz sentido, mas no R faz! E qual convenção se usa para que essa operação seja bem definida? A resposta é Reciclagem. O operador + é uma função vetorizada e que está programado para lidar com quase qualquer tipo de soma que o usuário queira desafiá-lo a fazer. Ao ser incumbido da árdua missão de somar dois vetores de tamanhos diferentes, o + "recicla" os valores do menor vetor, no caso o vetor x, reutilizando seus valores até preencher o vetor maior.

Esta convenção aparece sempre que possível no R e vale tomar cuidado: há vezes em que o R não avisa que reciclou valores.

Funções

Funções são grandes trunfos das linguagens de programação. Função no R tem a mesma finalidade das funções das demais linguagens: evitar repetir códigos e construir abstrações. Funções deixam o código mais legível, elegante e menos repetitivo. Além disso, funções abstraem uma rotina para casos mais gerais por meio de parâmetros, fazendo-a útil para casos além daquela configuração específica que motivou sua implementação.

Estrutura

nome_da_funcao <- function(<parâmetros>) {
  # faz coisas com os parâmetros
  resultado
}

# uso da função
nome_da_funcao(param1, param2, ...)

Pontos relevantes:

• Funções também são objetos! Aliás, tudo que você atribui com <- vira um objeto no R. Assim, é natural pensar que funções podem receber outras funções como argumento e isso é bem comum.

• Assim que uma função for atribuída a um objeto, use esta função como se ela tivesse vinda com o R: nome_da_funcao(...).

Parâmetros

Funções aceitam quaisquer e quantos parâmetros precisar e retorna um objeto, de qualquer tipo, inclusive nada (NULL). No lugar do <parâmetros> você pode colocar nomes que servirão de objetos (número, texto, vetor, lista, etc.) dentro da sua função.

Parâmetros opcionais

Parâmetros são objetos cujos valores devem ser atribuídos pelo usuário. Porém, existem parâmetros opcionais, que assumem um dado valor padrão caso o usuário opte por não especificar explicitamente.

# função que ecoa uma palavra
ecoar <- function(palavra, n_ecos = 3) {
    paste(c(rep(palavra, n_ecos), "!"), collapse = " ")
}

Parâmetros relativos

Além de parâmetros opcionais, podem existir parâmetros cujo valor padrão usa o valor de outro parâmetro. Exemplo:

# Função que desenha um histograma
histograma <- function(numeros, xlab = "x", titulo = paste("Histograma de", xlab)) {
  hist(numeros, xlab = xlab, main = titulo)
}

# Simula 1000 medidas de altura de pessoas de uma Normal com média 1,80 e desvio padrão de 0,1.
altura <- rnorm(n = 1000, mean = 1.80, sd = 0.1)
histograma(altura, "altura")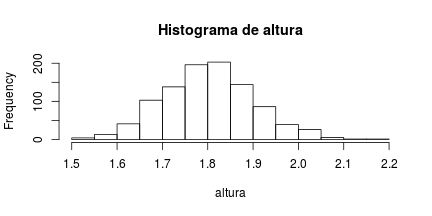

histograma(altura, "altura", "Eu escolho o título que eu quiser")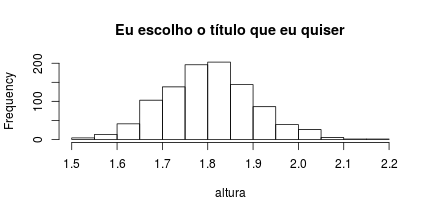

O parâmetro xlab define o título do eixo x enquanto titulo escreve o título principal do gráfico. Este último irá utilizar o nome passado para o eixo x para criar o seu valor padrão.

Ordem ou nome

Podemos passar valores aos parâmetros explicitamente ou implicitamente. Passar valor explicitamente significa associar o valor desejado ao nome do parâmetro. Por exemplo, no código rnorm(n = 1000, mean = 1.80, sd = 0.1) está claro qual valor será passado para cada parâmetro. Se quisermos omitir os nomes dos parâmetros, as funções terão a boa vontade de deduzir a qual parâmetro você deseja atribuir certo valor e isso é feito utilizando a ORDEM dos parâmetros definidos na criação da função. No comando histograma(altura, "altura") nenhum parâmetro foi diretamente definido, mas pela ordem, o vetor altura foi atribuído ao parâmetro numeros e a string "altura" foi atribuída ao parâmetro xlab da função histograma(). A versão "explícita" desse comando seria histograma(numeros = altura, xlab = "altura").

OBS: Misturar as formas, explícitas e implícitas, também funciona e versões explícitas aceitam que os parâmetros sejam passados fora de ordem. A expressão histograma(xlab = "altura", altura) daria certo também!

OBS 2: Se não for ambíguo, o R aceita que apenas parte do nome do parâmetro seja passado. No nosso exemplo, histograma(altura, t = "Eu escolho o título que eu quiser", x = "altura") levaria ao mesmo resultado que todos os citados até aqui.

Parâmetro "..."

Existe um parâmetro especial e frequentemente disponível em funções que é simbolizado por três pontinhos "...". Esse argumento indica que pode ser passado um número variável de parâmetros e que, geralmente, estes serão repassados para outras funções.

Uma utilidade é quando você deseja fazer possível mexer nos parâmetros de uma função, mas não quer copiar todos os seus parâmetros novamente. Retomemos o exemplo da função histograma():

histograma <- function(numeros, xlab = "x", titulo = paste("Histograma de", xlab), ...) {
  hist(numeros, xlab = xlab, main = titulo, ...)
}

histograma(altura, breaks = 100, col = 2)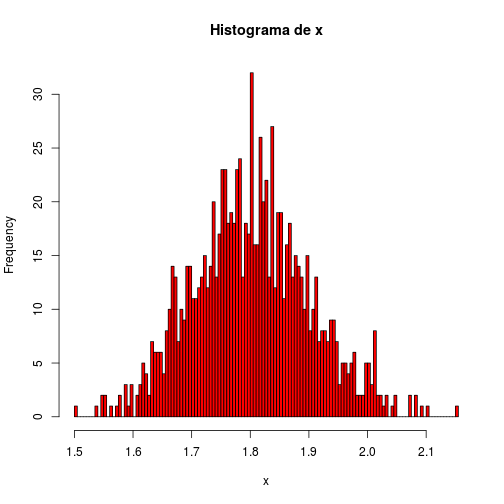

Repare que nunca precisamos definir os parâmetros breaks e col na função histograma(). O ... fez o trabalho de enviar essas informações à função hist().

Um segundo cenário que ... se faz útil é quando uma função aceita um número indefinido de argumentos. Um exemplo disso é a função paste(), que concatena palavras. A ela, podemos passar quantas palavras quisermos. Não fosse o ..., teríamos que ter os parâmetros (palavra1, palavra2, palavra3, ...). Sem chances.

args(paste)

## function (..., sep = " ", collapse = NULL) 
## NULL

paste("Eu", "sou", "o", "capitão", "planeta")

## [1] "Eu sou o capitão planeta"

Funções anônimas

As funções anônimas são frequentemente utilizadas e têm essa denominação pois não nos damos o trabalho de defini-las como um objeto permanente no nosso ambiente de trabalho. Veja o exemplo abaixo:

nums <- 1:10

eh_par <- sapply(nums, function(numero) {numero %% 2 == 0})

cbind(nums, eh_par) 

##       nums eh_par
##  [1,]    1      0
##  [2,]    2      1
##  [3,]    3      0
##  [4,]    4      1
##  [5,]    5      0
##  [6,]    6      1
##  [7,]    7      0
##  [8,]    8      1
##  [9,]    9      0
## [10,]   10      1

Não se preocupe em entender tudo o que o código acima está fazendo, você aprenderá adiante tudo sobre a função sapply() e cbind(). O ponto deste exemplo está na parte function(numero) {numero %% 2 == 0}. Este pedaço de código define uma função, mas essa função não tem nome! Apesar disso, ela continua sendo um objeto e pode ser passada como parâmetro de função, assim como faríamos com números, textos e vetores. Caso a função fosse útil em outros contextos ou tivesse que ser repetida em outra parte do código, poderíamos guardá-la no ambiente de trabalho, como mostra o exemplo que segue:

testa_se_eh_par <- function(numero) {
  numero %% 2 == 0
}

eh_par <- sapply(nums, testa_se_eh_par)

O resultado é idêntico como deveria ser, mas agora a função tem nome e pode ser utilizada conforme a conveniência.

Escopo

Objetos moram em ambientes (environments) e as funções as procuram os objetos que precisam usar nesses environments.

A ordem de procura segue a regra do mais específico até o ambiente global (.GlobalEnv) e se nada for encontrado, retorna um erro informando que não existe tal objeto.

Se houver dois objetos com o mesmo nome, prevalece aquele mais específico (o primeiro que for encontrado).

(x <- exp(1))

## [1] 2.718282

f <- function(x) print(x)
f(2)

## [1] 2

g <- function(y) print(x)
g(2)

## [1] 2.718282

No exemplo acima, o objeto x existe tanto fora, quanto dentro da função f(). Ao ser chamado para ser usado na função print(x), o objeto utilizado foi aquele que estava dentro do ambiente da função, que no caso foi atribuído com o valor 2.

O x que vale exp(1) está morando no global envirnment (.GlobalEnv) e seria utilizado apenas no caso em que nenhum outro x estivesse no caminho.

Na função g(), não existe mais o objeto x dentro dela (trocamos por y). O único objeto que está dentro de lá é o y. Como ainda chamamos pelo x dentro da função, o R irá buscar por ele, onde quer que ele esteja.

Variáveis Aleatórias

No R é muito fácil calcular f.d.p's, f.d.a's, quantis e até mesmo simular variáveis aleatórias das mais consagradas distribuições de probabilidade. O nome dessas funções segue um padrão que chamamos de funções (d, p, q, r). Exemplo para a distribuição Normal:

dnorm(x, mean = 0, sd = 1, log = FALSE)
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
rnorm(n, mean = 0, sd = 1)

Repare nas 4 letras que antecedem norm nos nomes das funções. Essas letras significam:

• d ("density") Densidade da Normal, ou f.d.p da Normal;
• p ("probability") Função de distribuição acumulada (f.d.a) da Normal;
• q ("quantile") Quantil da Normal;
• r ("random") Gera um número vindo de uma Normal.

No lugar de norm, você pode trocar por outra distribuição de probabilidade. A tabela abaixo lista algumas das possibilidades:

Para consultar a lista completa de distribuições da família (d, p, q, r), rode no console ?Distributions.

Vocabulário

Trigonometria

Matemática

Estatística

Diversos

Referências

http://adv-r.had.co.nz/Functions.html

http://www.burns-stat.com/pages/Tutor/R_inferno.pdf