Aula 09 - Laboratório III

Aula 09 - Laboratório III
2015-02-06
Source
Pacotes necessários para o Lab. III
```
library(ggplot2)
library(magrittr)
library(tidyr)
library(dplyr)
library(jpeg)
library(tree)
```
Laboratório III - Recuperação de imagem

Neste laboratório iremos comparar visualmente o desempenho de modelos de regressão linear e de árvores de decisão em duas diferentes situações.

Para isso, iremos mexer com imagens .jpg.

Imagens .jpg

Antes de iniciarmos a brincadeira, vale uma breve introdução às imagens .jpg, pois elas formarão os data.frame's do laboratório.

Arquivos com extenção .jpg guardam 5 coordenadas que são suficientes para serem entendidas e desenhadas pelo computador:
- x e y são as coordenadas cartesianas da imagem; e
- r, g e b red, green e blue, respectivamente, que juntas formam cores.
Todas as cores que conhecemos podem ser compostas pela combinação dessas três cores. A intensidade de cada cor varia de 0 a 1.

Para cada ponto no plano (x,y) existe uma cor associada. Assim, uma imagem pode ser representada por um banco de dados com 5 colunas: x, y, r, g e b.

Objetivo
- Verificar qual modelo entre regressão linear e árvores de decisão é o mais adequado para recuperar a o componente azul da imagem purple_wave.jpg.
- Verificar qual modelo entre regressão linear e árvores de decisão é o mais adequado para recuperar a o componente azul da imagem xadrez_colorido.jpg.
Preparação do Banco de dados
1. Para construir nossos bancos de dados, carregue as duas imagens abaixo (clique para download e salve na pasta do seu projeto):
  - purple_wave.jpg
  - xadrez_colorido.jpg
2. Com auxílio da função readJPEG() do pacote jpeg, carregue uma das imagens no R e transforme para data.frame (primeiro a purple_wave.jpg).
```
# a) carrega uma imagem jpeg no R 
img <- readJPEG("assets/fig/purple_wave.jpg")

# b) transforma o array da imagem em data.frame com infos de posicao (x,y) e cor (r,g,b)
# dimensões da imagem
img_dim <- dim(img)

# RGB para data.frame
img_df <- data.frame(
  x = rep(1:img_dim[2], each = img_dim[1]),
  y = rep(img_dim[1]:1, img_dim[2]),
  r = as.vector(img[,,1]),
  g = as.vector(img[,,2]),
  b = as.vector(img[,,3])
) %>%
  mutate(cor = rgb(r, g, b),
         id = 1:n())
```
1. Divida o data.frame em duas partes: uma com o azul (coluna b) e outra sem.
- Parte 1) x, y, r, g
- Parte 2) x, y, r, g, b
```
# para reprodução
set.seed(1) 

# Parte 1) x, y, r, g
img_df_parte1 <- img_df %>% 
  sample_frac(3/5) %>% # separando 3/5 do banco
  mutate(b_backup = b, # backup do azul original
         b = 0, # retirando o azul da imagem
         cor = rgb(r, g, b)) # cor da imagem sem o azul

# Parte 2) x, y, r, g, b
img_df_parte2 <- img_df %>% filter(!id%in%img_df_parte1$id) # filtra as linhas que estão na Parte 1
```
1. Visualize.
Veja como fica a imagem original sem o azul e como é o azul original isolado.
```
# Imagem sem o azul
ggplot(data = img_df_parte1, aes(x = x, y = y)) + 
  geom_point(colour = img_df_parte1$cor) +
  labs(x = "x", y = "y", title = "Imagem sem B (azul)") +
  coord_fixed(ratio = 1) +
  theme_bw()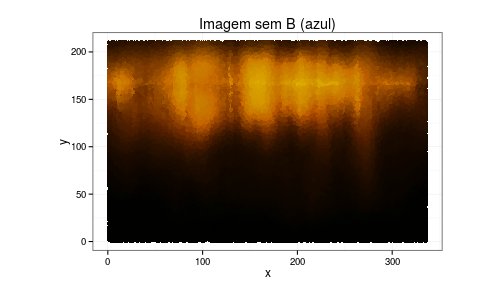
```
```
# Apenas o azul da imagem
ggplot(data = img_df_parte2, aes(x = x, y = y)) + 
  geom_point(colour = img_df_parte2$cor) +
  labs(x = "x", y = "y", title = "Imagem sem B (azul)") +
  coord_fixed(ratio = 1) +
  theme_bw()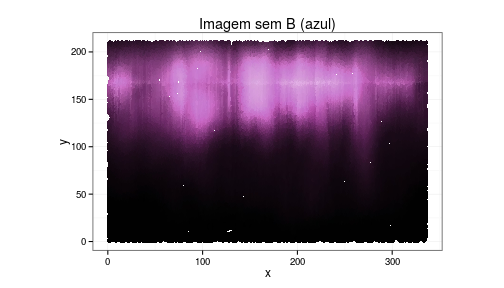
```
A sua tarefa é recuperar o azul (b) da Parte 1 que apagamos utilizando modelos preditivos construídos com a Parte 2 (que ainda tem o azul!). Vamos aos exercícios.

Exercícios

Exercício 1: Descritiva

Construa para x, y, r, g, b:
- A matriz de correlação linar e arredonde os resultados para duas casas decimais (utilize a função cor());
- A matriz de gráficos de dispersão (use a função pairs()).
DICA: faça esse exercício com uma amostra de 500 linhas do img_df, pois é muito pesado com o banco inteiro.
```
# uma amostra de 500 pontos para a análise descritiva (usar o banco inteiro é desnecessário e demorado)
img_df_amostra <- img_df %>% 
  sample_n(500,replace = FALSE)
```
Exercício 2: Modelo de Regressão Linear
- Com base na análise descritiva do exercício anterior, proponha um preditor para b e traduza para o R como uma fórmula;
- Ajuste uma regressão linear utilizando a fórmula proposta e a função lm();
LEMBRETE: fórmulas de modelos deixam a resposta à esquerda do ~ e as preditivas/explicativas à direita.

Exercício 3: Modelo de Árvore de Decisão
- Com base na análise descritiva do exercício anterior, escolha as variáveis para predizer b e passe como uma fórmula à função.
- Ajuste uma árvore de decisão por meio da função tree() do pacote tree, passando a fórmula com as variáveis escolhidas.
Exercício 4: Comparação
- Calcule o erro de predição.
- Desenhe o original e o predito.
- Qual ficou melhor?
- Você acha que o padrão da imagem (transições suaves de cor) influenciou neste resultado? Por quê?
Exercício 5: Outra Imagem
- Repita os exercícios de 1 a 4, mas agora para a imagem xadrez_colorido.jpg.
- Quanto ao desempenho para recuperar o azul de imagens, teve uma técnica melhor?
Exercício Extra (opcional): Imagens da Internet

Crie duas strings no R, link_lm e link_tree, cada uma contendo, respectivamente:
- Um link para uma imagem que seria bem recuperada pelo modelo de regressão linear.
- Um link para uma imagem que seria bem recuperada pelo modelo de árvore de decisão.

« Back Home